Let $f:\left[0, \frac{\pi}{2}\right] \rightarrow R: f(x)=\sin x$ and $g:\left[0, \frac{\pi}{2}\right] \rightarrow R: g(x)=\cos x$ Show that each one of $f$ and $g$ is one - one but $(f+g)$ is not one - one.
$f:\left[0, \frac{\pi}{2}\right] \rightarrow R: f(x)=\sin x$
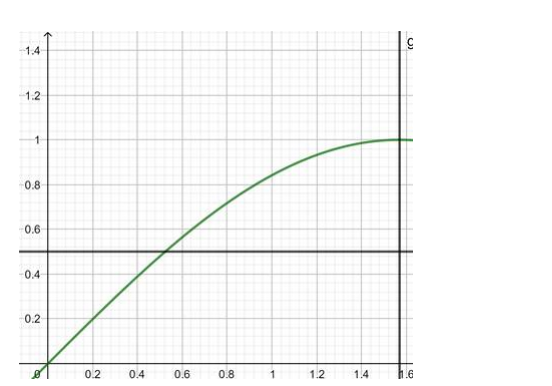
Here in this range, the lines do not cut the curve in 2 equal valued points of $y$, therefore, the function $f(x)=$ $\sin x$ is one - one.
$g:\left[0, \frac{\pi}{2}\right] \rightarrow R: g(x)=\cos x$
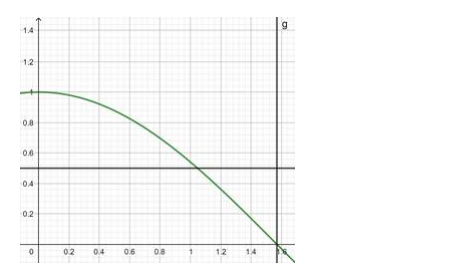
in this range, the lines do not cut the curve in 2 equal valued points of $y$, therefore, the function $f(x)=$ cosx is also one - one.
$(f+g):\left[0, \frac{\pi}{2}\right] \rightarrow R=\sin x+\cos x$
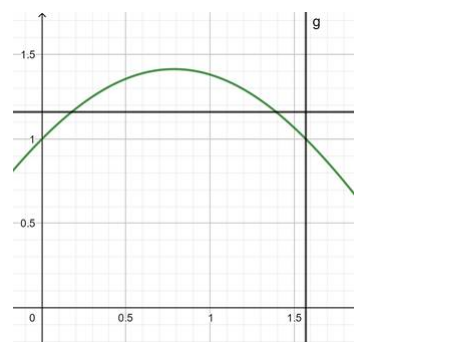
in this range the lines cut the curve in 2 equal valued points of $y$, therefore, the function $f(x)=$ cosx $+$ sin $x$ is not one - one.
Hence,showed that each one of $f$ and $g$ is one - one but $(f+g)$ is not one - one.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.