Question:
Prove that in a triangle, other than an equilateral triangle, angle opposite the longest side is greater than $\frac{2}{3}$ of a right angle.
Solution:
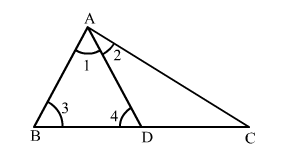
Given: In
To prove: $\angle B A C>\frac{2}{3}$ of a right angle, i.e., $\angle B A C>60^{\circ}$
Construct: Mark a point D on side AC such that AD = AB = BD.
Proof:
In
$\therefore \angle 1=\angle 3=\angle 4=60^{\circ}$
Now
$\angle B A C=\angle 1+\angle 2=60^{\circ}+\angle 2$
but $60^{\circ}=\frac{2}{3}$ of a right angle
So, $\angle B A C=\frac{2}{3}$ of a right angle $+\angle 2$
Hence, $\angle B A C>\frac{2}{3}$ of a right angle.
