Question.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Solution:
ABCD is a square having sides of length = a.
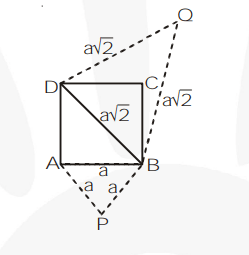
Then the diagonal $\mathrm{BD}=\mathrm{a} \sqrt{2}$.
We construct equilateral $\Delta \mathrm{s}$ PAB and QBD
$\Rightarrow \Delta \mathrm{PAB} \sim \Delta \mathrm{QBD}$ (Equilateral triangles are similar)
$\Rightarrow \frac{\operatorname{ar}(\Delta \mathrm{PAB})}{\operatorname{ar}(\Delta \mathrm{OBD})}=\frac{A B^{2}}{B D^{2}}=\frac{a^{2}}{(a \sqrt{2})^{2}}=\frac{1}{2}$
$\Rightarrow$ ar $(\Delta \mathrm{PAB})=\frac{1}{2}$ ar $(\Delta \mathrm{QBD})$
Tick the correct answer and justify
ABCD is a square having sides of length = a.
Then the diagonal $\mathrm{BD}=\mathrm{a} \sqrt{2}$.
We construct equilateral $\Delta \mathrm{s}$ PAB and QBD
$\Rightarrow \Delta \mathrm{PAB} \sim \Delta \mathrm{QBD}$ (Equilateral triangles are similar)
$\Rightarrow \frac{\operatorname{ar}(\Delta \mathrm{PAB})}{\operatorname{ar}(\Delta \mathrm{OBD})}=\frac{A B^{2}}{B D^{2}}=\frac{a^{2}}{(a \sqrt{2})^{2}}=\frac{1}{2}$
$\Rightarrow$ ar $(\Delta \mathrm{PAB})=\frac{1}{2}$ ar $(\Delta \mathrm{QBD})$
Tick the correct answer and justify