Question:
Prove that the circles described with the four sides of a rhombus, as diameters, pass through the point of intersection of its diagonals.
Solution:
Let ABCD be the rhombus with AC and BD as diagonals intersecting at point O.
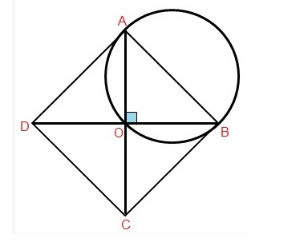
The diagonals of a rhombus bisect each other at right angles.
i.e., ∠AOB = ∠BOC = ∠COD = ∠AOD = 90°
Now, circles with AB, BC, CD and DA as diameter passes through O (angle in a semi-circle is a right angle).
Hence, the circle with four sides of a rhombus as diameter, pass through O, i.e., the point of intersection of its diagonals.
