Prove that the internal bisector of an angle of a triangle divides

Solution:

Let the triangle be $\mathrm{ABC}$ with $\mathrm{AD}$ as the bisector of $\angle A$ which meets $\mathrm{BC}$ at $\mathrm{D}$.

We have to prove:

$\frac{B D}{D C}=\frac{A B}{A C}$

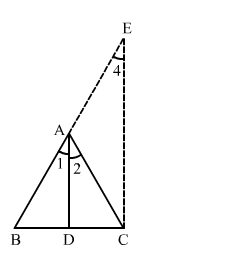
Draw CE ∥">∥DA, meeting BA produced at E.
CE ∥">∥DA
Therefore,

$\angle 2=\angle 3 \quad$ (Alternate angles)

and $\angle 1=\angle 4 \quad$ (Corresponding angles)

But,

$\angle 1=\angle 2$

Therefore,

$\angle 3=\angle 4$

$\Rightarrow A E=A C$

In $\triangle B C E, D A \| C E$.

Applying Thales' theorem, we gave:

$\frac{B D}{D C}=\frac{A B}{A E}$

$\Rightarrow \frac{B D}{D C}=\frac{A B}{A C}$

This completes the proof.