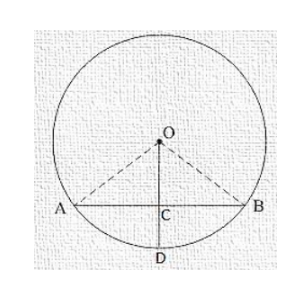
Prove that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the
Question:
Prove that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
Solution:
Given:
C is the mid-point of chord AB.
To prove: D is the mid-point of arc AB.
Proof:
In ΔOAC and ΔOBC
OA = OB [Radius of circle]
OC = OC [Common]
AC = BC [C is the mid-point of AB]
Then ΔOAC ≅ ΔOBC [By SSS condition]
∴ ∠AOC = ∠BOC
$\Rightarrow \mathrm{m} \overline{\mathrm{A}} \mathrm{D} \cong \mathrm{m} \overline{\mathrm{B}} \mathrm{D}$
$\Rightarrow \overline{\mathrm{A}} \mathrm{D} \cong \overline{\mathrm{B}} \mathrm{D}$
Hence, D is the mid-point of arc AB.