Prove that the tangent drawn at the mid-point

Let mid-point of an arc AMB be M and TMT’ be the tangent to the circle.

Join AB, AM and MB.

Since, $\operatorname{arc} A M=\operatorname{arc} M B$

Chord $A M=$ Chord $M B$

$\ln \triangle A M B$ $A M=M B$

$\Rightarrow \quad \angle M A B=\angle M B A$

[equal sides corresponding to the equal angle] ... (i)

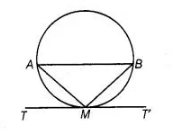
Since, $T M T^{\prime}$ is a tangent line.

$\therefore \quad \angle A M T=\angle M B A$

[angles in alternate segments are equal]

$=\angle M A B \quad$ [from Eq. (i)]

But ∠AMT and ∠MAB are alternate angles, which is possible only when

AB∥TMT’

Hence, the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc

Hence proved.