Question:
Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
Solution:
To prove ∠1 = ∠2, let PQ be a chord of the circle. Tangents are drawn at the points R and Q.
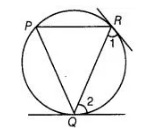
Let P be another point on the circle, then, join PQ and PR.
Since, at point Q, there is a tangent.
$\therefore$ $\angle 2=\angle P \quad$ [angles in alternate segments are equal]
Since, at point $R$, there is a tangent.
$\therefore$ $\angle 1=\angle P$ [angles in alternate segments are equal]
$\therefore$ $\angle 1=\angle 2=\angle P$
Hence proved.