Prove that the tangents drawn at the ends of the diameter of a circle are parallel.

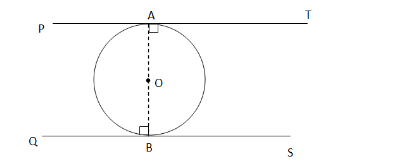
Here, $P T$ and $Q S$ are the tangents to the circle with centre $O$ and $A B$ is the diameter.

Now, radius of a circle is perpendicular to the tangent at the point of contact.

$\therefore \mathrm{OA} \perp \mathrm{AT}$ and $\mathrm{OB} \perp \mathrm{BS}$ (since tangents drawn from an external point are

perpendicular to the radius at point of contact)

$\cdot \angle O A T=\angle O B O=90^{\circ}$

But $\angle O A T$ and $\angle O B Q$ are alternate angles.

$\therefore A T$ is parallel to $B S$.