Question:
Let a vector $\alpha \hat{\mathrm{i}}+\beta \hat{\mathrm{j}}$ be obtained by rotating the vector $\sqrt{3} \hat{\mathrm{i}}+\hat{\mathrm{j}}$ by an angle $45^{\circ}$ about the origin in counterclockwise direction in the first quadrant. Then the area of triangle having vertices $(\alpha, \beta),(0, \beta)$ and $(0,0)$ is equal to
Correct Option: 1
Solution:
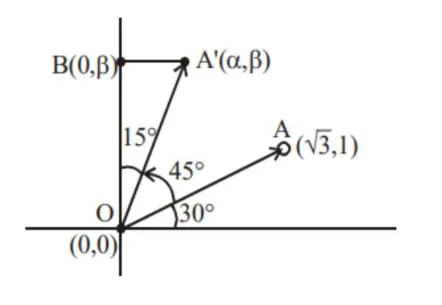
Area of $\Delta\left(\mathrm{OA}^{\prime} \mathrm{B}\right)=\frac{1}{2} \mathrm{OA}^{\prime} \cos 15^{\circ} \times \mathrm{OA}^{\prime} \sin 15^{\circ}$
$=\frac{1}{2}\left(\mathrm{OA}^{\prime}\right)^{2} \frac{\sin 30^{\circ}}{2}$
$=(3+1) \times \frac{1}{8}=\frac{1}{2}$
