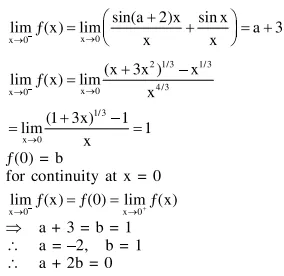Question: If $f(x)= \begin{cases}\frac{\sin (a+2) x+\sin x}{x} ; & x<0 \\ b & ; x=0 \\ \frac{\left(x+3 x^{2}\right)^{\frac{1}{3}}-x^{\frac{1}{3}}}{x^{\frac{4}{3}}} & ; x>0\end{cases}$
is continuous at $x=0$, then $a+2 b$ is equal to :
Correct Option: , 4
Solution: