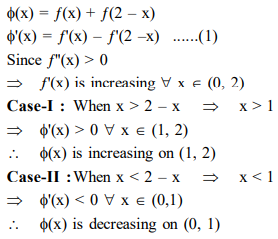Question: Let $f:[0,2] \rightarrow \mathrm{R}$ be a twice differentiable function such that $f^{\prime \prime}(\mathrm{x})>0$, for all $\mathrm{x} \in(0,2)$. If $\phi(x)=f(x)+f(2-x)$, then $\phi$ is :
decreasing on $(0,2)$
decreasing on $(0,1)$ and increasing on $(1,2)$
increasing on $(0,2)$
increasing on $(0,1)$ and decreasing on $(1,2)$
Correct Option: , 2
Solution: