Question:
Let $S=\left\{\theta \in[-2 \pi, 2 \pi]: 2 \cos ^{2} \theta+3 \sin \theta=0\right\}$. Then the sum of the elements of $S$ is:
Correct Option: , 3
Solution:
$2 \cos ^{2} \theta+3 \sin \theta=0$
$\Rightarrow(2 \sin \theta+1)(\sin \theta-2)=0$
$\Rightarrow \sin \theta=-\frac{1}{2}$ or $\sin \theta=2 \rightarrow$ Not possibe
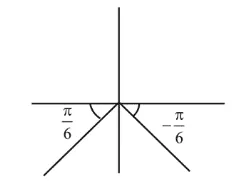
The required sum of all solutions in $[-2 \pi, 2 \pi]$ is
$=\left(\pi+\frac{\pi}{6}\right)+\left(2 \pi-\frac{\pi}{6}\right)+\left(-\frac{\pi}{6}\right)+\left(-\pi+\frac{\pi}{6}\right)=2 \pi$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.