Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass:

Solution:

(a)Take a system of i moving particles.

Mass of the $i^{\text {th }}$ particle $=m_{i}$

Velocity of the $i^{\text {th }}$ particle $=\mathbf{v}_{i}$

Hence, momentum of the $i^{\text {th }}$ particle, $\mathbf{p}_{i}=m_{i} \mathbf{v}_{i}$

Velocity of the centre of mass $=\mathrm{V}$

The velocity of the $t^{\text {th }}$ particle with respect to the centre of mass of the system is given as:

$\mathbf{v}_{i}^{\prime}=\mathbf{v}_{i}-\mathbf{V}$

$\mathbf{v}_{i}^{\prime}=\mathbf{v}_{i}-\mathbf{v} \ldots(1)$

Multiplying $m_{i}$ throughout equation $(1)$, we get:

$m_{i} \mathbf{v}_{i}^{\prime}=m_{i} \mathbf{v}_{i}-m_{i} \mathbf{v}$

$\mathbf{p}_{i}^{\prime}=\mathbf{p}_{i}-m_{i} \mathbf{V}$

Where,

$\mathbf{p}_{i}{ }^{\prime}=m_{i} \mathbf{v}_{i}{ }^{\prime}=$ Momentum of the $i^{\text {th }}$ particle with respect to the centre of mass of the system

$\therefore \mathbf{p}_{i}=\mathbf{p}_{i}^{\prime}+m_{i} \mathbf{V}$

We have the relation: $\mathbf{p}_{i}{ }^{\prime}=m_{i} \mathbf{v}_{i}{ }^{\prime}$

Taking the summation of momentum of all the particles with respect to the centre of mass of the system, we get:

$\sum_{i} \mathbf{p}_{i}^{\prime}=\sum_{i} m_{i} \mathbf{v}_{i}^{\prime}=\sum_{i} m_{i} \frac{d \mathbf{r}_{i}^{\prime}}{d t}$

Where,

$\mathbf{r}^{\prime},=$ Position vector of $i$ th particle with respect to the centre of mass

$\mathbf{v}_{t}^{\prime}=\frac{d \mathbf{r}^{\prime}}{d t}$

As per the definition of the centre of mass, we have:

$\sum m_{i} \mathbf{r}_{i}^{\prime}=0$

$\therefore \sum_{j} m_{j} \frac{d \mathbf{r}^{\prime},}{d t}=0$

$\sum_{i} p_{1}^{\prime}=0$

(b) We have the relation for velocity of the $i^{\text {th }}$ particle as:

$\mathbf{v}_{i}=\mathbf{v}_{i}^{\prime}+\mathbf{V}$

$\sum_{i} m_{i} \mathbf{v}_{i}=\sum_{i} m_{i} \mathbf{v}_{i}^{\prime}+\sum_{i} m_{i} \mathrm{~V}$

Taking the dot product of equation

 

$\sum m_{i} \mathbf{v}_{i} \sum m_{i} \mathbf{v}_{i}=\sum m_{i}\left(\mathbf{v}_{;}^{\prime}+\mathbf{v}\right) \cdot \sum m_{i}\left(\mathbf{v}_{i}^{\prime}+\mathbf{v}\right)$

$M^{2} \sum_{i} v_{i}^{2}=M^{2} \sum_{i} v_{i}^{2}+M^{2} \sum_{i} \mathbf{v}_{i} \cdot \mathbf{v}_{i}^{\prime}+M^{2} \sum \mathbf{v}_{i}^{\prime} \cdot \mathbf{v}_{i}+M^{2} V^{2}$

Here, for the centre of mass of the system of particles, $\sum_{i} \mathbf{v}_{i} \mathbf{v}_{,}^{\prime}=-\sum_{i} \mathbf{v}_{i}^{\prime} \mathbf{v}_{i}$

$M^{2} \sum_{i} v_{i}^{2}=M^{2} \sum_{i} v_{i}^{2}+M^{2} V^{2}$

$\frac{1}{2} M \sum v_{i}^{2}=\frac{1}{2} M \sum v_{i}^{\prime 2}+\frac{1}{2} M V^{2}$

$K=K^{\prime}+\frac{1}{2} M V^{2}$

Where,

$K=\frac{1}{2} M \sum v_{i} v_{i}^{2}=$ Total kinetic energy of the system of particles

$K=\frac{1}{2} M \sum_{i} v_{i}^{\prime 2}=$ Total kinetic energy of the system of particles with respect to the centre of mass

$\frac{1}{2} M V^{2}=$ Kinetic energy of the translation of the system as a whole

(c) Position vector of the $t^{\text {th }}$ particle with respect to origin $=\mathbf{r}_{i}$

Position vector of the $i^{\text {th }}$ particle with respect to the centre of mass $=\mathbf{r}_{i}$

Position vector of the centre of mass with respect to the origin $=\mathbf{R}$

It is given that:

$\mathbf{r}_{i}^{\prime}=\mathbf{r}_{j}-\mathbf{R}$

$\mathbf{r}_{i}=\mathbf{r}_{i}{ }_{i}+\mathbf{R}$

We have from part (a),

$\mathbf{p}_{i}=\mathbf{p}_{i}^{\prime}+m_{i} \mathbf{V}$

Taking the cross product of this relation by $\mathbf{r}_{i}$, we get:

$\sum \mathbf{r}_{i} \times \mathbf{p}_{i}=\sum \mathbf{r}_{i} \times \mathbf{p}^{\prime},+\sum_{i} \mathbf{r}_{i} \times m_{j} \mathbf{V}$

$\mathbf{L}=\sum_{i}\left(\mathbf{r}_{i}^{\prime}+\mathbf{R}\right) \times \mathbf{p}_{i}^{\prime}+\sum_{i}\left(\mathbf{r}_{i}^{\prime}+\mathbf{R}\right) \times m_{i} \mathbf{V}$

$=\sum_{i} \mathbf{r}_{i}^{\prime} \times \mathbf{p}_{i}^{\prime}+\sum_{i} \mathbf{R} \times \mathbf{p}^{\prime},+\sum_{i} \mathbf{r}_{i}^{\prime} \times m_{i} \mathbf{V}+\sum_{i} \mathbf{R} \times m_{i} \mathbf{V}$

$=\mathbf{L}^{\prime}+\sum_{i} \mathbf{R} \times \mathbf{p}^{\prime},+\sum_{i} \mathbf{r}^{\prime}, \times m_{j} \mathbf{V}+\sum_{i} \mathbf{R} \times m_{i} \mathbf{V}$

Where,

$\mathbf{R} \times \sum \mathbf{p}_{i}^{\prime}=0$ and

$\left(\sum_{i} \mathbf{r}_{i}^{\prime}\right) \times M \mathbf{V}=\mathbf{0}$

$\sum m_{i}=M$

$\therefore \mathbf{L}=\mathbf{L}^{\prime}+R \times M \mathbf{V}$

(d) We have the relation:

$\mathbf{L}^{\prime}=\sum \mathbf{r}^{\prime}, \times \mathbf{p}^{\prime}$

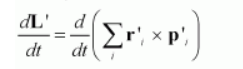
$=\frac{d}{d t}\left(\sum_{i} \mathbf{r}_{\prime}^{\prime}\right) \times \mathbf{p}^{\prime},+\sum_{i} \mathbf{r}_{\prime}^{\prime}, \times \frac{d}{d t}\left(\mathbf{p}_{\prime}^{\prime}\right)$

$=\frac{d}{d t}\left(\sum_{i} m, \mathbf{r}_{\prime}^{\prime}\right) \times \mathbf{v}_{,}^{\prime}+\sum_{i} \mathbf{r}_{,}, \times \frac{d}{d t}\left(\mathbf{p}_{\prime}^{\prime}\right)$

Where, $\mathbf{r}^{\prime}$, is the position vector with respect to the centre of mass of the system of particles.

$\therefore \sum m_{i} \mathbf{r}_{\prime}^{\prime}=0$

$\therefore \frac{d \mathbf{L}^{\prime}}{d t}=\sum_{1} \mathbf{r}_{1}^{\prime} \times \frac{d}{d t}\left(\mathbf{p}_{1}^{\prime}\right)$

We have the relation:

$\frac{d \mathbf{L}^{\prime}}{d t}=\sum_{i} \mathbf{r}^{\prime}, \times \frac{d}{d t}\left(\mathbf{p}^{\prime}\right)$

$=\sum_{i} \mathbf{r}_{i}^{\prime} \times m_{i} \frac{d}{d t}\left(\mathbf{v}_{i}^{\prime}\right)$

Where, $\frac{d}{d t}\left(\mathbf{v}_{i}^{\prime}\right)$ is the rate of change of velocity of the $i$ th particle

with respect of the centre of mass of the system

Therefore, according to Newton's third law of motion, we can write:

i.e., $\sum_{i} \mathbf{r}_{i}^{\prime} \times m_{i} \frac{d}{d t}\left(\mathbf{v}_{i}^{\prime}\right)=\tau_{\text {ext }}^{\prime}=$ External torque acting on the system as a whole

$\therefore \frac{d \mathbf{L}^{\prime}}{d t}=\tau_{\mathrm{ext}}^{\prime}$