Show graphically that each one of the following systems of equations has infinitely many solutions:

The given equations are

$3 x+y=8$...(i)

$6 x+2 y=16$...(ii)

Putting $x=0$ in equation $(i)$, we get:

$\Rightarrow 3 \times 0+y=8$

$\Rightarrow y=8$

$x=0, \quad y=8$

Putting $y=0$ in equations $(i)$ we get:

$\Rightarrow 3 x+0=8$

$\Rightarrow x=8 / 3$

$x=8 / 3, \quad y=0$

Use the following table to draw the graph.

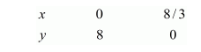
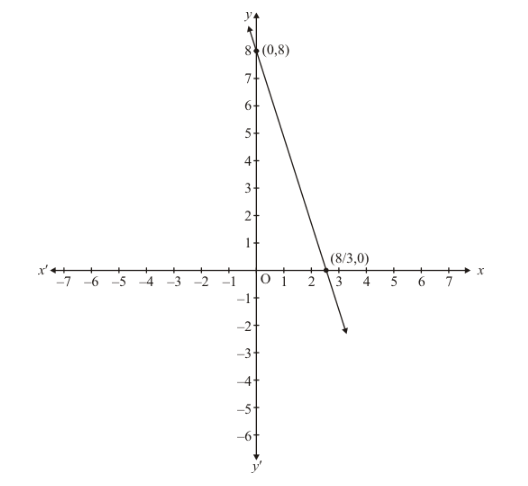
Draw the graph by plotting the two points $A(0,8)$ and $B(8 / 3,0)$ from table.

Graph of the equation….

$6 x+2 y=16$ ...(ii)

Putting $x=0$ in equations $(i i)$ we get:

$\Rightarrow 6 \times 0+2 y=16$

$\Rightarrow y=8$

$x=0, \quad y=8$

Putting $y=0$ in equation $(i i)$, we get:

$\Rightarrow 6 x+2 \times 0=16$

$\Rightarrow x=8 / 3$

$x=8 / 3, \quad y=0$

Use the following table to draw the graph.

Draw the graph by plotting the two points $C(0,8), D(8 / 3,0)$ from table.

Thus the graph of the two equations coincide 

Consequently, every solution of one equation is a solution of the other.

Hence the equations have infinitely many solutions.