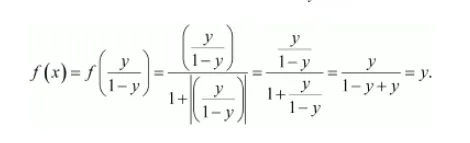Show that function f: R → {x ∈ R: −1 < x < 1} defined by f(x) =,

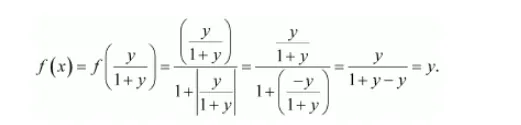
It is given that $f: \mathbf{R} \rightarrow\{x \in \mathbf{R}:-1

Suppose $f(x)=f(y)$, where $x, y \in \mathbf{R}$.

$\Rightarrow \frac{x}{1+|x|}=\frac{y}{1+|y|}$

It can be observed that if x is positive and y is negative, then we have:

$\frac{x}{1+x}=\frac{y}{1-y} \Rightarrow 2 x y=x-y$

Since x is positive and y is negative:

$x>y \Rightarrow x-y>0$

But, 2xy is negative.

Then, $2 x y \neq x-y$.\

Thus, the case of x being positive and y being negative can be ruled out.

Under a similar argument, x being negative and y being positive can also be ruled out

 x and y have to be either positive or negative.

When x and y are both positive, we have:

$f(x)=f(y) \Rightarrow \frac{x}{1-x}=\frac{y}{1-y} \Rightarrow x-x y=y-y x \Rightarrow x=y$

$\therefore f$ is one-one.

Now, let $y \in \mathbf{R}$ such that $-1

If $x$ is negative, then there exists $x=\frac{y}{1+y} \in \mathbf{R}$ such that

If $x$ is positive, then there exists $x=\frac{y}{1-y} \in \mathbf{R}$ such that

∴ f is onto.

Hence, f is one-one and onto.