Show that the following system of linear equations has no solution:

We have:

$x+2 y \leq 3 \quad \ldots \ldots(\mathrm{i})$

$3 x+4 y \geq 12 \quad \ldots$ (ii)

$x \geq 0 \quad \ldots$ (iii)

$y \geq 1 \quad \ldots \ldots$ (iv)

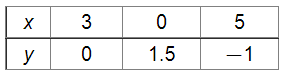
As, the points satisfying x + 2y = 3 are:

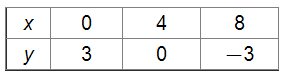
Also, the points satisfying 3x + 4y = 12 are:

Now, the region representing the given inequalities is as follows:


Since, there is no common region.

So, the given system of inequalities has no solution.