Show that the function

To show: $f: R \rightarrow R: f(x)=x^{4}$ is many $-$ one into.

Proof:

$f(x)=x^{4}$

$\Rightarrow y=x^{4}$

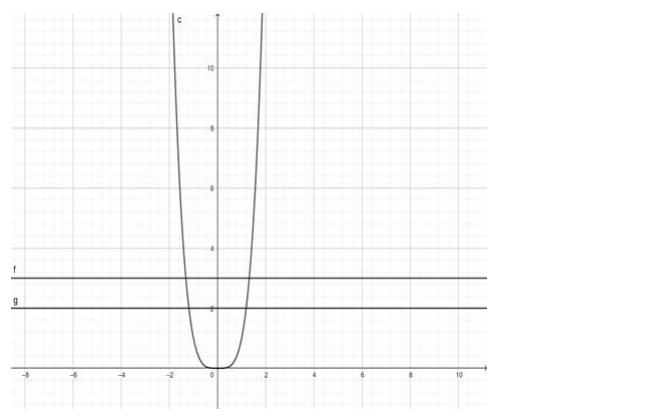
Since the lines cut the curve in 2 equal valued points of $y$, therefore, the function $f(x)$ is many ones.

The range of $f(x)=[0, \infty) \neq R($ Codomain $)$

$\therefore f(x)$ is not onto

$\Rightarrow f(x)$ is into

Hence, showed that $f: R \rightarrow R: f(x)=x^{4}$ is many - one into.