Show that the quadrilateral formed by joining the midpoints of the pairs of adjacent sides of a square is a square.

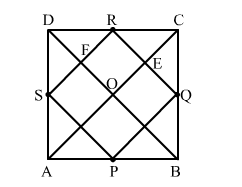
Let ABCD be a square and P, Q, R and S be the midpoints of AB, BC, CD and DA, respectively. 
Join the diagonals AC and BD. Let BD cut SR at F and AC cut RQ at E. Let O be the intersection point of AC and BD.

In ∆ ABC, we have:

$\therefore P Q \| A C$ and $P Q=\frac{1}{2} A C$      [By midpoint theorem]

Again, in ∆DAC, the points S and R are the midpoints of AD and DC, respectively.

$\therefore S R \| A C$ and $S R=\frac{1}{2} A C$    [By midpoint theorem]

Now, PQ ∣∣ AC and SR ∣∣ AC  ⇒ PQ ∣∣ SR

Also, PQ = SR         [ Each equal to $\frac{1}{2} \mathrm{AC}$ ]    (i)

So, PQRS is a parallelogram.

Now, in ∆SAP and ∆QBP, we have:
AS = BQ   
∠A = ∠B = 90o
AP = BP
i.e.,  ∆SAP ≅ ∆QBP​
∴ PS = PQ                  ...(ii)
Similarly, ∆SDR ≅ ∆RCQ​
∴ SR = RQ                 ...(iii)
From (i), (ii) and (iii), we have:
PQ = PS = SR = RQ           ...(iv)

We know that the diagonals of a square bisect each other at right angles.
∴ ∠​EOF = 90o
​Now, RQ ∣∣ DB 
⇒RE ∣∣ FO
Also, SR ∣∣ AC
⇒FR ∣∣ OE
∴ OERF is a parallelogram. 
So, ∠FRE = ∠EOF = 90o​         (Opposite angles are equal)
Thus, PQRS is a parallelogram with ∠R = 90o and PQ = PS = SR = RQ.

 ∴​ PQRS is a square.