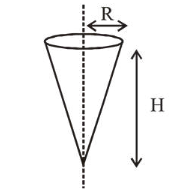
Shown in the figure is a hollow icecream cone(it is open at the top).

(4) Hollow ice-cream cone can be assume as several parts of discs having different radius, so

$I=\int d I=\int d m\left(r^{2}\right)$ ...(i)

From diagram,

$\frac{r}{h}=\tan \theta=\frac{R}{H}$ or $r=\frac{R}{H} h$      ...(ii)

Mass of element, $d m=\rho\left(\pi r^{2}\right) d h$    ...(iii)

From eq. (i), (ii) and (iii),

Area of element, $d A=2 \pi r d l=2 \pi r \frac{d h}{\cos \theta}$

Mass of element, $d m=\frac{2 M h \tan d h}{R \sqrt{R^{2}+H^{2}} \cos \theta}$

(here, $r=h \tan \theta$ )

$I=\int d I=\int_{0}^{H} d m\left(r^{2}\right)=\int_{0}^{H} \rho\left(\pi r^{2}\right) d h\left(\frac{R}{H} \cdot h\right)^{2}$

$=\int_{0}^{H} \rho\left(\pi\left(\frac{R}{H} \cdot h\right)^{4}\right)^{4} d h$

Solving we get, $I=\frac{M R^{2}}{2}$