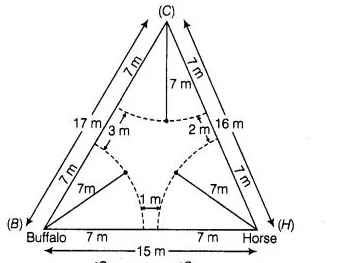
Sides of a triangular field are 15 m, 16m and 17m.

Given that, a triangular field with the three corners of the field a cow, a buffalo and a horse are tied separately with ropes. So, each animal grazed

the field in each corner of triangular field as a sectorial form.

Given, radius of each sector (r) = 7m

Now, area of sector with $\angle C=\frac{\angle C}{360^{\circ}} \times \pi r^{2}=\frac{\angle C}{360^{\circ}} \times \pi \times(7)^{2} \mathrm{~m}^{2}$

Area of the sector with $\angle B=\frac{\angle B}{360^{\circ}} \times \pi r^{2}=\frac{\angle B}{360^{\circ}} \times \pi \times(7)^{2} \mathrm{~m}^{2}$

and area of the sector with $\angle H=\frac{\angle H}{360^{\circ}} \times \pi r^{2}=\frac{\angle H}{360^{\circ}} \times \pi \times(7)^{2} \mathrm{~m}^{2}$

Therefore, sum of the areas $\left(\right.$ in $\left.\mathrm{cm}^{2}\right)$ of the three sectors

$=\frac{\angle C}{360^{\circ}} \times \pi \times(7)^{2}+\frac{\angle B}{360^{\circ}} \times \pi \times(7)^{2}+\frac{\angle H}{360^{\circ}} \times \pi \times(7)^{2}$

$=\frac{(\angle C+\angle B+\angle H)}{360^{\circ}} \times \pi \times 49 .$

$=\frac{180^{\circ}}{360^{\circ}} \times \frac{22}{7} \times 49=11 \times 7=77 \mathrm{~cm}^{2}$

Given that, sides of triangle are $a=15, b=16$ and $c=17$

Now, semi-perimeter of triangle, $s=\frac{a+b+c}{2}$

$\Rightarrow$ $=\frac{15+16+17}{2}=\frac{48}{2}=24$

$\therefore$ Area of triangular field $=\sqrt{s(s-a)(s-b)(s-c)}$ [by Heron's formula]\

$=\sqrt{24 \cdot 9 \cdot 8 \cdot 7}$

$=\sqrt{64 \cdot 9 \cdot 21}$

$=8 \times 3 \sqrt{21}=24 \sqrt{21} \mathrm{~m}^{2}$

So, area of the field which cannot be grazed by the three animals

$=$ Area of triangular field - Area of each sectorial field

$=24 \sqrt{21}-77 \mathrm{~m}^{2}$

Hence, the required area of the field which can not be grazed by the three animals is $(24 \sqrt{21}-77) \mathrm{m}^{2}$.