Solve each of the following system of equations in R.

$\frac{4}{x+1} \leq 3 \leq \frac{6}{x+1}, x>0$

$\Rightarrow \frac{4}{x+1} \leq 3$ and $3 \leq \frac{6}{x+1}$

Now,

$\frac{4}{x+1} \leq 3$

$\Rightarrow \frac{4}{x+1}-3 \leq 0$

$\Rightarrow \frac{4-3 x-3}{x+1} \leq 0$

$\Rightarrow \frac{1-3 x}{x+1} \leq 0$

$\Rightarrow \frac{3 x-1}{x+1} \geq 0$

$\Rightarrow x \in(-\infty,-1) \cup\left[\frac{1}{3}, \infty\right)$

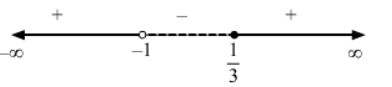
Thus, the solution set of the inequation is $(-\infty,-1) \cup\left[\frac{1}{3}, \infty\right)$.

And,

$\frac{6}{x+1} \geq 3$

$\Rightarrow \frac{6}{x+1}-3 \geq 0$

$\Rightarrow \frac{6-3 x-3}{x+1} \geq 0$

$\Rightarrow \frac{3-3 x}{x+1} \geq 0$

$\Rightarrow \frac{3 x-3}{x+1} \leq 0$

$\Rightarrow x \in(-1,1]$

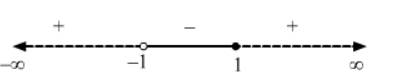
Thus, the solution set of the inequation is $(-1,1]$.

The common values of $x$ in both the inequation is $\left[\frac{1}{3}, 1\right]$.

Hence, the solution set of both the inequation is $\left[\frac{1}{3}, 1\right]$.