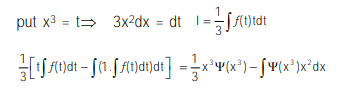Question: If $\int f(\mathrm{x}) \mathrm{dx}=\Psi(\mathrm{x})$, then $\int \mathrm{x}^{5} f\left(\mathrm{x}^{3}\right) \mathrm{dx}$ is equal to :
$\frac{1}{3}\left[x^{3} \Psi\left(x^{3}\right)-\int x^{2} \Psi\left(x^{3}\right) d x\right]+C$
$\frac{1}{3} \mathrm{x}^{3} \Psi\left(\mathrm{x}^{3}\right)-3 \int \mathrm{x}^{3} \Psi\left(\mathrm{x}^{3}\right) \mathrm{dx}+\mathrm{C}$
$\frac{1}{3} x^{3} \Psi\left(x^{3}\right)-\int x^{2} \Psi\left(x^{3}\right) d x+C$
$\frac{1}{3}\left[x^{3} \Psi\left(x^{3}\right)-\int x^{3} \Psi\left(x^{3}\right) d x\right]+C$
Correct Option: , 3
Solution: