Question:
The students $S_{1}, S_{2}, \ldots, S_{10}$ are to be divided into 3 groups $A, B$ and $C$ such that each group has at least one student and the group $C$ has at most 3 students. Then the total number of possibilities of forming such groups is
Solution:
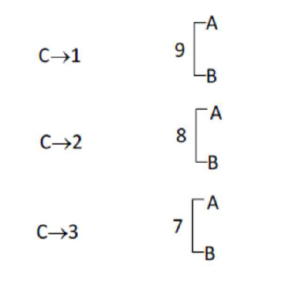
$={ }^{10} C_{1}\left[2^{9}-2\right]+{ }^{10} C_{2}\left[2^{8}-2\right]+{ }^{10} C_{3}\left[2^{7}-2\right]$
$=2^{7}\left[{ }^{10} C_{1} \times 4+{ }^{10} C_{2} \times 2+{ }^{10} C_{3}\right]-20-90-240$
$=128[40+90+120]-350$
$=(128 \times 250)-350$
$=10[3165]=31650$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.