Solve the following :

Question:

A disc of radius $R$ is cut out from a larger disc of radius $2 R$ in such a way that the edge of the hole touches the edge of the disc. Locate the center of mass of the residual disc.

Solution:

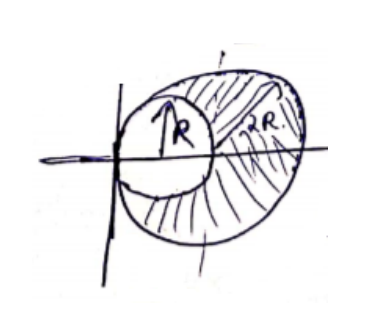
C.O.M of $2 \mathrm{R}$ disc $=(2 \mathrm{R}, 0)$

C.O.M of R disc $=(R, 0)$

$=\frac{m_{n} R_{n} R-m_{R} R_{R}}{m_{n} R-m_{R}}$

$=\frac{\rho 4 \pi l R^{2}(8 R-R)}{\rho 4 \pi l R^{2}(4-1)}=\frac{7 R}{3}$

From C.O.M of $2 R$ disc, it is $\frac{7 R}{3}-2 R=\frac{R}{3}$ distance away.

Leave a comment

None

All Study Material

Free Study Material