A hemispherical bowl of radius $R$ is rotated about its axis of symmetry which is kept vertical. A small block is kept in the bowl at a position where the radius makes an angle $\theta$ with the vertical. The block rotates with the bowl without any slipping. The friction coefficient between the block and the bowl surface is $u$. Find the range of the angular speed for which the block will not slip.
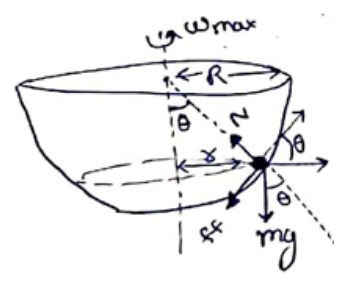
Particle will have tendency to move up. So, frictional force is in downward direction. $r=R \sin \theta-\cdots(i)$
$\mathrm{N}=\mathrm{mg} \cos \theta+m r w_{\max }^{2} \sin \theta \cdots->(\mathrm{ii})$
$\mathrm{ff}+m q \sin \theta=m r w_{\max }^{2} \cos \theta \cdots>$ (iii)
$\mathrm{ff}=\mu \mathrm{N} \cdots \cdots$ (iv)
on solving,
$\omega_{\max _{x}}=\left[\frac{g(\sin \theta+\mu \cos \theta)}{R \sin \theta(\cos \theta-\mu \sin \theta)}\right]$
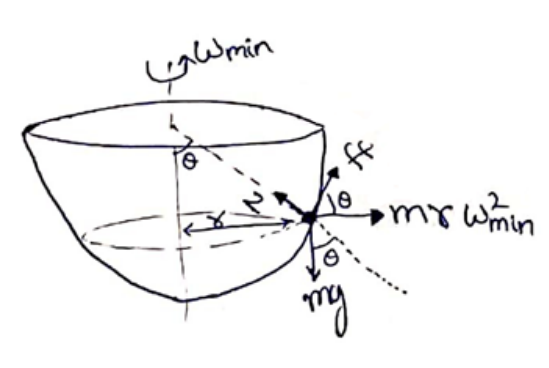
For $\omega_{\min }$, particle will have tendency to move down. So, frictional force acting upward direction.
$r=R \sin \theta-\cdots(1)$
$\mathrm{N}=\mathrm{mg} \cos \theta+m r w_{\min }^{2} \sin \theta-\cdots>(\mathrm{ii})$
$M g \sin \theta=\mathrm{ff}+{ }^{m r} w_{\min }^{2} \cos \theta-\cdots>($ iii)
$\mathrm{ff}=\mu \mathrm{N} \cdots->$ (iv)
on solving,
$\omega_{\min }=\left[\frac{g(\sin \theta-\mu \cos \theta)}{R \sin \theta(\cos \theta+\mu \sin \theta)}\right]$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.