A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity $c o$ in a circular path of radius $R$ (figure 7-E3). A smooth groove $A B$ of length $L(« R)$ is made on the surface of the table. The groove makes an angle 0 with the radius $\mathrm{OA}$ of the circle in which the cabin rotates. $A$ small particle is kept at the point $A$ in the groove and is released to move along $A B$. Find the time taken by the particle to reach the point $B$.
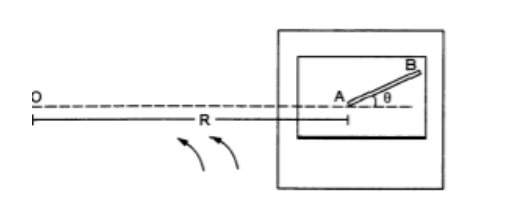
Component of force $m R \omega^{2}$ along the line $A B$ will be responsible for motion of particle Force $=m R \omega^{2} \cos \theta$
$m a=m R \omega^{2} \cos \theta$
$a=R \omega^{2} \cos \theta$
$u=0$
$s=L$
using $s=u t+\frac{1}{2} a t^{2}$
$I=\frac{1}{2}\left(R \omega^{2} \cos \theta\right) t^{2}$
$t=\frac{2 L}{R \omega^{2} \cos \theta}$
