Seven homogeneous bricks, each of length $L$, are arranged in shown in figure. Each brick is displaced with respect to the one in contact by $L / 10$. Find the $x$-coordinate of the center of mass relative to the origin shown.
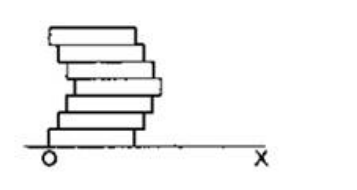
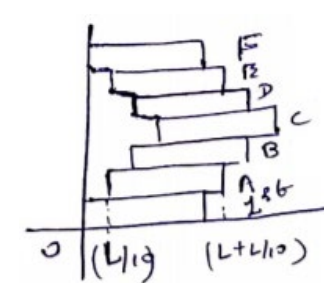
take $O$ as $(0,0)$
brick $A$ and $E$ is from $\left(\frac{L}{10}\right.$ to $\left.L+\frac{L}{10}\right)$
brick $B$ and $D$ is from $\left(\frac{2 L}{10}\right.$ to $\left.L+\frac{2 L}{10}\right)$
brick $C$ is from $\left(\frac{3 L}{10}\right.$ to $\left.L+\frac{3 L}{10}\right)$
$1^{\text {st }}, F$ are from $(0$ to $L)$
For $1^{s t}$ and F bricks, C.O.M= $\left(\frac{L}{2}\right)$
For $B$ and D, C.O.M $=\left(\frac{L}{2}+\frac{2 L}{10}\right)$
(as they are displaced by $\frac{}{\frac{2 L}{10}}$ )
Similarly,
For $A$ and E C.O.M $=\left(\frac{L}{2}+\frac{L}{10}\right)$
For C, C.O.M $=\left(\frac{L}{2}+\frac{3 L}{10}\right)$
