Two balls having masses $\mathrm{m}$ and $2 \mathrm{~m}$ are fastened to two light strings of same length I. The other ends of the strings are fixed at $O$. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a) Find the velocities of the balls just after their collision. (b) How high will the balls rise after the collision?
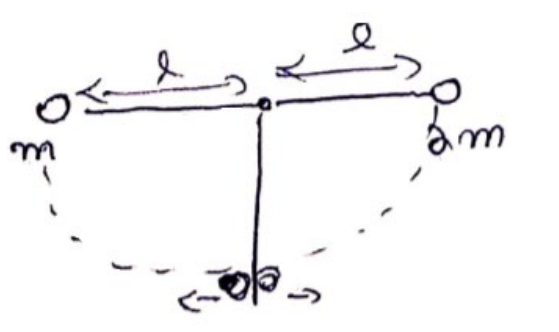
(a) For initial velocities,
Use C.O.E.L
$\frac{1}{2} m V_{1}^{2}=m g l$
$V_{1}=\sqrt{2 g l}$
$\frac{1}{2}(2 m) V_{2}^{2}=(2 m) g l$
Use C.O.L.M
$m \cdot V_{1}+2 m V_{2}=m V_{1}^{\prime}+(2 m) V_{2}^{\prime}$
$m(\sqrt{2 g l})+2 m(-\sqrt{2 g l})=m V_{1}^{\prime}+(2 m) V_{2}^{\prime}$
$V_{1}^{\prime}+2 V_{2}^{\prime}=-\sqrt{2 g l}$
$\therefore V_{1}-V_{2}=V_{2}^{2}-V_{1}^{2}$
$V_{1}^{\circ}-V_{2}^{\sigma}=-V_{1}+V_{2}$
$=-(\sqrt{2 g l}-(-\sqrt{2 g l}))$
$=-2 \sqrt{2 g l}$
Solve (1) and (2)
$-3 V_{2}^{\prime}=-\sqrt{2 g l} \Longrightarrow V_{2}^{\prime}=\frac{\sqrt{2 g l}}{3}$
Similarly,
$V_{1}^{\prime}=\frac{\sqrt{50 g l}}{3}$
(b) Use C.O.E.L
$\frac{1}{2} 2 m(0)^{2}-\frac{1}{2} 2 m\left(V_{2}\right)^{2}=-2 m g h$
$$
\Rightarrow h=\frac{l}{9}
$$
For mass m, use C.O.E.L,
$\frac{1}{2} m(0)^{2}-\frac{1}{2} m\left(V_{1}^{\prime}\right)^{2}=m g h^{\circ}$
$g h^{\prime \prime}=\frac{1}{2} \frac{50 g l}{9}$
$h^{\prime}=\frac{25 l}{9}$
$2 \mathrm{~m}$ will rise $u n$ to $h=\frac{l}{9}$
$\mathrm{m}$ will rise up to
$h^{\prime}=\frac{25 l}{9}$
