A semi-circular wire has a length $\mathrm{L}$ and mass $\mathrm{M}$. A particle of mass $\mathrm{m}$ is placed at the centre of the circle.
Find the gravitational attraction on the particle due to the wire.
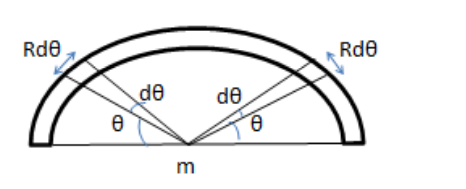
Consider two small elements at an angle $\theta$ from horizontal length of the element $=\mathrm{Rd} \theta$
Mass of each element $\mathrm{dm}=\frac{M}{L}(\mathrm{Rd} \theta)$
Force by elemental mass on particle
$\mathrm{dF}=\frac{\mathrm{Gm}(\mathrm{dm})}{R^{2}}$
$\mathrm{dF}=\frac{\mathrm{GmM}(\mathrm{Rd \theta})}{R^{2} L}$
$\mathrm{dF}=\frac{\mathrm{GmM}}{R L} d \theta$
Resultant of the both elemental forces $=2 \mathrm{dF} \sin \theta$ Net Force
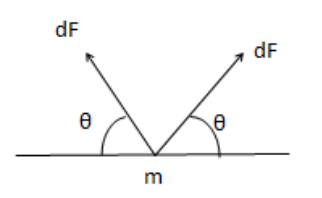
$\mathrm{F}_{\mathrm{N}}=\int 2 \mathrm{dF} \sin \theta$
$=\int_{0}^{\frac{\pi}{2}} 2\left(\frac{\mathrm{Gm} M}{R L}\right) d \theta \sin \theta$
$=2 \frac{\mathrm{Gm} M}{R L}[-\cos \theta]_{0}^{\pi / 2}$
$=2 \frac{\mathrm{Gm} M}{R L}$
$\mathrm{F}_{\mathrm{N}=} \frac{2 \pi \mathrm{GmM}}{L^{2}}($ because $\pi R=L)$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.