A tunnel is dug along a chord of the earth at a perpendicular distance $R / 2$ from the earth's center. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass $m$ when it is at a distance $x$ from the center of the tunnel.
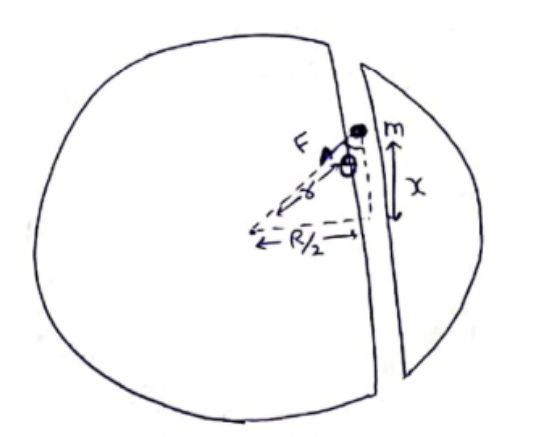
Distance of the particle from earth's center
$r=\sqrt{\left(\frac{R}{2}\right)^{2}+x^{2}}$
Force on the particle=mass ${ }^{X}$ gravitational field intensity
$F=m\left(\frac{G M r}{R^{3}}\right)$
$G=\frac{G M m}{R^{3}} r$
Force exerted by wall on particle=Force exerted by particle on wall
$=F \sin \theta$
$=\frac{G M m r}{R^{3}}\left(\frac{R}{2 r}\right)$
$=\frac{G M m}{2 R^{2}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.