A $6.5 \mathrm{~m}$ long ladder rests against a vertical wall reaching a height of $6.0 \mathrm{~m}$. A $60 \mathrm{~kg}$ man stands half way up the ladder. (a) Find the torque of the force exerted by the man on the ladder about the upper end of the ladder. (b)Assuming the weight of the ladder to be negligible as compared to the man and assuming the wall to be smooth, find the force exerted by the ground on the ladder.
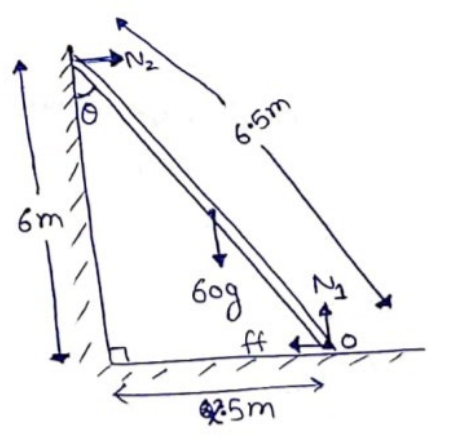
By Pythagoras theorem,
$(6.5)^{2}=(6)^{2}+B^{2}$
$B=2.5 \mathrm{~m}$
(a) $\tau=F \times d_{\Perp}$
$\mathrm{T}=6 \lg _{6.5}\left(\frac{6.5}{2} \sin \theta\right.$
$=60 \mathrm{~g}\left(\frac{2.5}{6.5}\right)$
$=60 \mathrm{~g}\left(\frac{6.5}{2} \times \frac{2.5}{6.5}\right)$
$\tau=740 \mathrm{~N}-\mathrm{m}$
(b) $N_{1}=60 g$
(Vertical Translatory Equation)
Rotational Equilibrium at $O$
$N_{2}(6.5 \cos \theta)=60 g\left(\frac{6.5}{2} \sin \theta\right)$
$N_{2}=30 g \tan \theta$
$N_{2}=30 g\left(\frac{2.5}{6}\right)$
$N_{2}=120 \mathrm{~N}$
