A person stands on a spring balance at the equator. (a) By what fraction is the balance reading less than his true weight? (b) If the speed of earth's rotation is increased by such an amount that the balance reading is half the true weight, what will be the length of the day in this case?
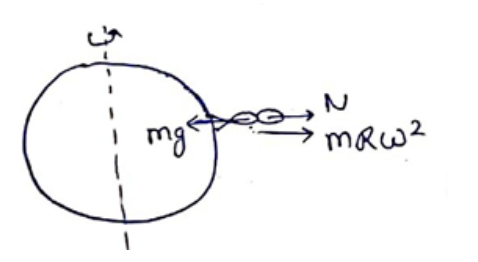
(a)
At equator, normal contact force $\mathrm{N}+\mathrm{mR} \omega^{2}=\mathrm{mg}$
Reading $N=m g-m R \omega^{2}$
$t=\frac{m g-\left(m g-m R w^{2}\right)}{m g}$
$\begin{aligned} & \frac{R w^{2}}{g} \\=& \frac{3}{3} \end{aligned}$
$=3.5 \times 10-3$
(b)
Balance reading $=\overline{2}$ (True weight)
$m g-m R \omega^{2}=\frac{1}{2}((m g)$
$\mathrm{mR} \omega^{2}=\frac{m g}{2}$
$\omega=\sqrt{\frac{\mathrm{g}}{2 R}}=\frac{2 \pi}{T r}$
$T^{\prime}=2 \times 3.14 \times \quad$ (in sec)
$T^{\prime}=\frac{2 \times 3.14 \times \sqrt{\frac{\left(6.4 \times 10^{7}\right)}{49}}}{(60 \times 60)}$
$\mathrm{T}^{\prime}=2 \mathrm{hrs}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.