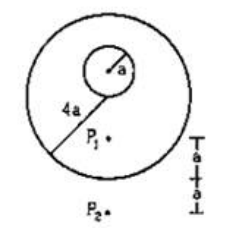
A uniform metal sphere of radius a and mass $\mathrm{M}$ is surrounded by a thin uniform spherical shell of equal mass and radius $4 a$ (figure 11-E2). The center of the shell falls on the surface of the inner sphere. Find the gravitational field at the points $P_{1}$ and $P_{2}$ shown in the figure.
(a) At point $P_{1}$
Net gravitational field=field due to shell+ field due to sphere
$\vec{E}_{N}=0+\frac{G M}{(a+4 a-a)^{2}}$
$\vec{E}_{N}=\frac{G M}{16 a^{2}}$
(b) At point $P_{2}$
Net gravitational field=field due to shell+ field due to sphere
$\vec{E}_{N}=\frac{G M}{(4 a+a)^{2}}+\frac{G M}{(4 a+a+a)^{2}}$
$\vec{E}_{N}=\frac{G M}{25 a^{2}}+\frac{G M}{36 a^{2}}$
$\vec{E}_{N}=\frac{61 G M}{900 a^{2}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.