Solve the following :

Question:
A car goes on a horizontal circular road of radius $\mathrm{R}$, the speed increasing at a constant rate $\mathrm{dv} / \mathrm{dt}=$ a. The friction dt coefficient between the road and the tyre is $\mu$. Find the speed at which the car will skid.

Solution:

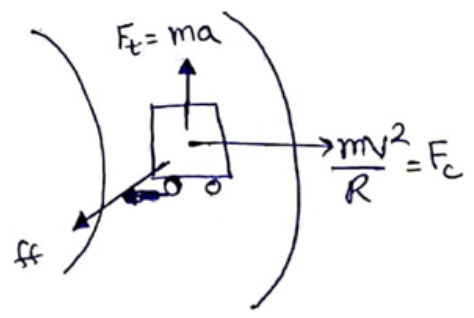
From free body diagram

$\mathrm{ff}=\sqrt{\left(F_{t}^{2}+F_{c}^{2}\right)}$

$\mu \mathrm{N}=\sqrt{(m a)^{2}+\left(\frac{m v^{2}}{R}\right)^{2}}$

$(\mu \mathrm{mg})=\sqrt{(m a)^{2}+\left(\frac{m v^{2}}{R}\right)^{2}}$

Squaring and solving,

$V=\left[\left(\mu^{2} g^{2}-a^{2}\right) R^{2}\right]^{1 / 4}$

Solve the following :

Leave a comment

All Study Material