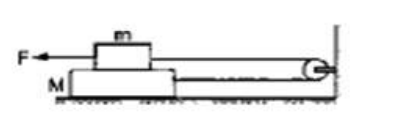
The friction coefficient between the two blocks shown in figure is $\mu$ but the floor is smooth.
(a) What maximum horizontal force F can be applied without disturbing the equilibrium of the system?
(b) Suppose the horizontal force applied is double of that found in part (a) Find the accelerations of the two masses.
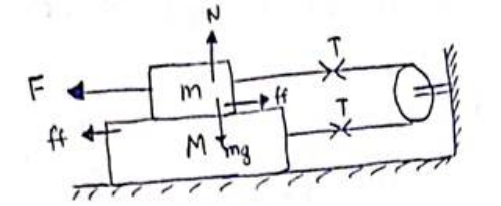
(a)For block m;
$\mathrm{N}=\mathrm{mg}$
$\mathrm{ff}=\mu \mathrm{N}=\mu \mathrm{mg}$
$\mathrm{F}=\mathrm{T}+\mathrm{ff}(\therefore$ acceleration $=\mu)$-(i)
For block M;
T=ff ( $\therefore$ acceleration $=0)$-(ii)
Solving (i)and(ii),
$\mathrm{F}=\mathrm{ff}+\mathrm{ft}$
$F=2$ uma
(b) Now applied force is $F=2(2 \mu \mathrm{mg})=4 \mu \mathrm{mg}$ For block m;
F-T-ff=ma -(i)
For block M;
T-ff=Ma -(ii)
Adding (i)and(ii),
$F-2 f f=(m+M) a$
$a=\frac{2 \mu m g}{(m+M)}$ in opposite directions.
