Three particles of masses $1.0 \mathrm{~kg}, 2.0 \mathrm{~kg}$ and $3.0 \mathrm{~kg}$ are placed at the corners $A, B$ and $C$ respectively of an equilateral triangle $A B C$ of edge $1 \mathrm{~m}$. Locate the center of mass of the system.
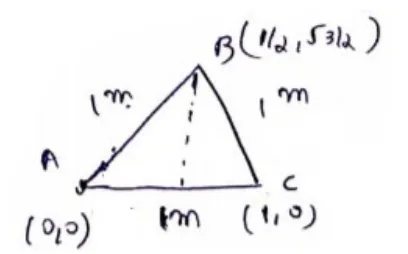
Take $A$ as origin $(0,0)$ then $C=(1,0)$
$B=\left(\frac{1}{2}, \sqrt{1-\left(\frac{1}{2}\right)^{2}}\right)=\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)$
$x_{C O M}=\frac{x_{A} m_{A}+m_{B} x_{B}+m_{C} x_{C}}{m_{A}+m_{B}+m_{C}}=\frac{1 .(0)+2\left(\frac{1}{2}\right)+3(1)}{6}$
$=\frac{4}{6}=\frac{2}{3}$
$y_{C O M}=\frac{y_{A} m_{A}+m_{B} y_{B}+m_{C} y_{C}}{m_{A}+m_{B}+m_{C}}=\frac{0+\frac{\sqrt{3}}{2} \cdot 2+0 .(3)}{6}$
$=\frac{\sqrt{3}}{6}$
$\left(x_{\text {COM }}, y_{\operatorname{COM}}\right)=\left(\frac{2}{3}, \frac{\sqrt{3}}{6}\right)$ if we take $A C$ as $x$-axis.
Similarly, if we take $A B$ as $x$-axis,
$\left(x_{\text {COM }} y_{C O M}\right)=\left(\frac{7}{12}, \frac{\sqrt{3}}{4}\right)$
