A train starts from rest and moved with a constant acceleration of $2.0 \mathrm{~m} / \mathrm{s}^{2}$ for half a minute. The brakes are then applied and the train comes to rest in one minute.
(a) Find the total distance moved by the train
(b) The maximum speed attained by the train
(c) The position(s) of the train at half the maximum speed.
A $=$ slope $=\frac{v}{t}$
$2=\frac{v}{30}$
$\mathrm{v}=60 \mathrm{~m} / \mathrm{s}$
(a) Distance=Area of v-t graph
$=\frac{1^{\prime}}{2}(30+60)(50)$
$=2700 \mathrm{~m}$
$=2.7 \mathrm{~km}$
(b) Maximum speed $\mathrm{V}=60 \mathrm{~m} / \mathrm{s}$
(C)
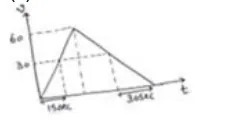
Velocity $30 \mathrm{~m} / \mathrm{s}$ is achieved at $\mathrm{t}=15 \mathrm{sec}$ and $\mathrm{t}=60 \mathrm{sec}$ Area of (v-t) graph in first 15 second
$s=\frac{1}{2}(15)(30)=225 \mathrm{~m}$
$=2250 \mathrm{~m}$
$=2.25 \mathrm{~km}$
