A solid sphere of mass $m$ and radius $r$ is placed inside a hollow thin spherical shell of mass $M$ and radius $\mathrm{R}$ as shown in figure (11-E1). A particle of mass $\mathrm{m}^{\prime}$ is placed on the line joining the two centers at a distance $x$ from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if (a) $r
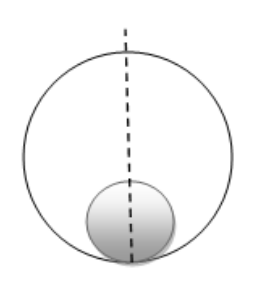
(a)
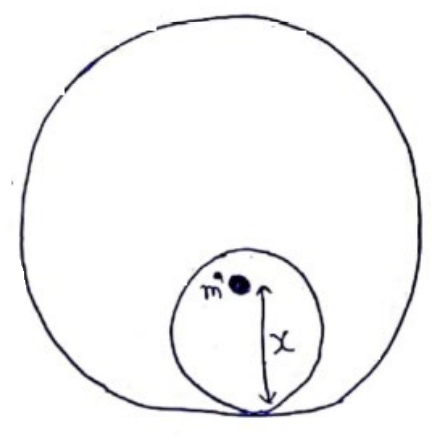
Gravitational field intensity inside shell is zero. So, force by shell on mass $m^{z}$ is zero. Now, for solid sphere.
Gravitational field inside sphere at a distance ( $x-r)$ from center is
$E=\frac{G m}{r^{3}}(x-r)$
So, force by sphere on mass $m^{z}$ is
$F=\frac{G m m^{\prime}}{r^{3}}(x-r)$
Net force
$\vec{F}_{N}=\vec{F}_{s p h e r e}+\vec{F}_{\text {shell }}$
$F_{N}=\frac{G m m^{\prime}(r-x)}{r^{3}}$
(b)
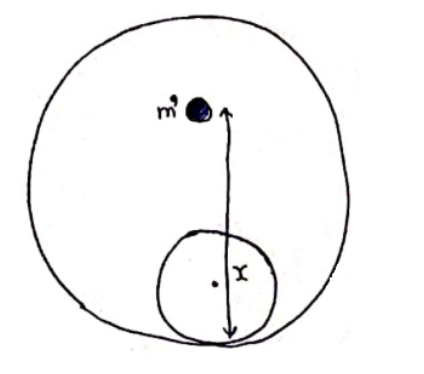
Gravitational field intensity inside shell is zero. So, force by shell on mass $m^{\prime}$ is zero. Now, for solid sphere.
Gravitational field intensity outside sphere at distance (x-r) is given by
$E=\frac{G m}{(x-r)^{2}}$
So, force by sphere on mass $m^{\prime}$ is
$F=m^{l} E$
$F=\frac{G m m^{\prime}}{(x-r)^{2}}$
Net force
$\vec{F}_{N}=\vec{F}_{s p h e r e}+\vec{F}_{\text {shell }}$
$F_{N}=\frac{G m m^{\prime}}{(x-r)^{2}}$
(c)
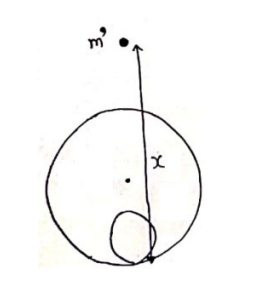
Force=mass ${ }^{\times}$Gravitational field intensity
Force by shell= $m^{\prime}\left(\frac{G M}{(x-R)^{2}}\right)$
(towards center)
Force by sphere $=m^{7}\left(\frac{\mathrm{Gm}}{(x-R)^{2}}\right)$ (towards center)
$\vec{F}_{\text {Net }}=\vec{F}_{\text {sphere }}+\vec{F}_{\text {shell }}$
$\vec{F}_{\text {Net }}=\frac{G m m^{\prime}}{(x-R)^{2}}+\frac{G M m^{\prime}}{(x-R)^{2}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.