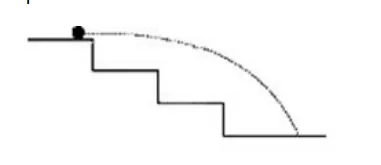
A staircase contains three steps each $10 \mathrm{~cm}$ high and $20 \mathrm{~cm}$ wide as shown in figure. What should be the minimum horizontal velocity of a hall rolling off the uppermost plane so as to hit directly the lowest plane?
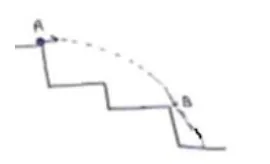
For minimum velocity ball will just be touching point $B$ If $A$ is origin then coordinates of $B(40,-20)$
$\mathrm{Y}=\mathrm{x} \tan \theta-\frac{1}{2} \frac{\mathrm{x}^{2}}{\mathrm{~g}^{\mathrm{u}^{2} \cos ^{2} \theta}}$
$-20=40 \tan 0^{\circ}-\frac{1}{2} \frac{\mathrm{g}(40)^{2}}{\mathrm{u}^{2} \cos ^{2} 0^{2}}$
$\mathrm{u}=200 \mathrm{~cm} / \mathrm{s}$
$\mathrm{u}=2 \mathrm{~m} / \mathrm{s}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.