Question:
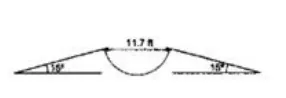
The given figure shows a $11.7 \mathrm{ft}$ wide ditch with the approach roads at tan angle of $15^{\circ}$ with the horizontal. With what minimum speed should a motorbike be moving on the roads so that it safely crosses the ditch?
Assume that the length of the bike is $5 \mathrm{ft}$ and it leaves the road when the front part runs out of the approach road.
Solution:
Range to be covered by bike $=11.7+5=16.7 \mathrm{ft}$
$\mathrm{R}=\frac{\mathrm{u}^{2} \sin 2 \theta}{2 \mathrm{~g}}$
$16.6=\frac{\mathrm{u}^{2} \sin (2 \times 15)}{2(32)}$
$\mathrm{u}=32 \mathrm{ft} / \mathrm{sec}$
