Derive an expression for the gravitational field due to a uniform rod of length $L$ and mass $M$ at a point on its perpendicular bisector at a distance $d$ from the centre.
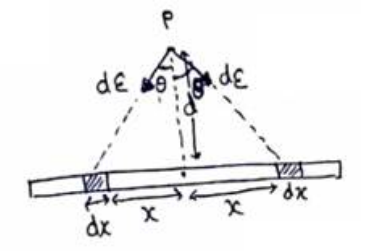
Consider two small elements of length $\mathrm{dx}$ at a distance $x$ from center on both sides of center.
Mass of each element, $\mathrm{dm}=\frac{M}{L} \mathrm{dx}$ Field due to each element at point $P$
$=\frac{G d m}{\sqrt{\left(d^{2}+x^{2}\right)^{2}}}$
$d E=\frac{G d m}{d^{2}+x^{2}}$
Resultant of the elemental field $=2 \mathrm{dE} \cos \theta$
Net electric force $=\int \frac{\mathrm{Gdm}}{\mathrm{d}^{2}+x^{2}}\left(\frac{\mathrm{d}}{\sqrt{\mathrm{d}^{2}+x^{2}}}\right.$
$\begin{aligned} & \int \frac{2 \mathrm{GdM} \cdot \mathrm{dx}}{L\left(\mathrm{~d}^{2}+x^{2}\right)^{\mathrm{s} / 2}} \\=& \frac{2 \mathrm{GdM}}{L} \int_{0}^{\frac{L}{2}}\left(\frac{\mathrm{dx}}{\left(\mathrm{d}^{2}+x^{2}\right)^{\mathrm{s} / 2}}\right) \\=& \frac{2}{L}=\end{aligned}$
On integrating,
$E_{N}=\frac{2 \mathrm{GdM}}{\mathrm{d}^{\sqrt{D^{2}+4 d^{2}}}}$
