Question:
The door of an almirah is $6 \mathrm{ft}$ high, $1.5 \mathrm{ft}$ wide and weighs $8 \mathrm{~kg}$. The door is supported by two hinges situated at a distance of $1 \mathrm{ft}$ from the ends. If the magnitudes of the force exerted by the hinges on the door are equal, find this magnitude.
Solution:
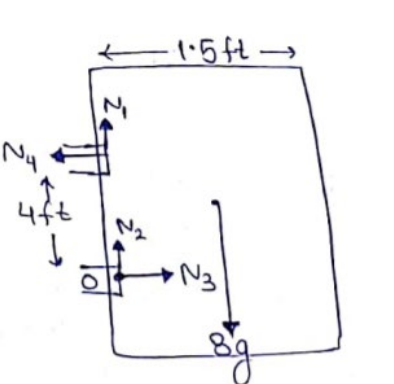
Magnitude of forces by hinges are equal.
$\sqrt{N_{1}^{2}+N_{4}^{2}}=\sqrt{N_{2}^{2}+N_{3}^{2}}$
$N_{1}^{2}+N_{4}^{2}=N_{2}^{2}+N_{3}^{2}-(\mathrm{i})$
Rotational Equilibrium at point $O$
$N_{4}(4)=8 g\left(\frac{1.5}{2}\right)$
$N_{4}=1.5 \mathrm{~g}$
Bv translational Equilibrium
$N_{3}=N_{4}=1.5 g$-(ii)
$N_{1}+N_{2}=8 g$
Solving (i),(ii),(iii)
$N_{1}=N_{2}=4 g$
Magnitude of force $=\sqrt{N_{1}^{2}+N_{4}^{2}}$
$=\sqrt{(4 g)^{2}+(1.5 g)^{2}}$
$=43 \mathrm{~N}$
