The pulley shown in figure has a radius of $20 \mathrm{~cm}$ and moment of inertia $0.2 \mathrm{~kg}^{-} \mathrm{m}^{2}$. The string going over it is attached at one end to a vertical spring of spring constant $50 \mathrm{~N} / \mathrm{m}$ fixed from below, and supports a $1 \mathrm{~kg}$ mass at the other end. The system is released from rest with the spring at its natural length. Find the speed of the block when it has descended through $10 \mathrm{~cm}$. Take $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}$.
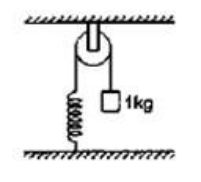
By energy conservation
$m g h=\frac{1}{2} m v^{2}+\frac{1}{2} k x^{2}+\frac{1}{2} I \omega^{2}$
$1^{\times} g \times(0.1)=\frac{1}{2}(1)(v)^{2}+\frac{1}{2}(50)(0.1)^{2}+\frac{1}{2}(0.2) \frac{v^{2}}{(0.2)^{2}}$
$\mathrm{v}=0.5 \mathrm{~m} / \mathrm{s}$
