Question:
A kid of mass $M$ stands at the edge of a platform of radius $R$ which can be freely rotated about its axis. The moment of inertia of the platform is $\mathrm{I}$. The system is at rest when a friend throws a ball of mass $m$ and the kid catches it. If the velocity of the ball is $v$ horizontally along the tangent to the edge of the platform when it was caught by the kid, find the angular speed of the platform after the event.
Solution:
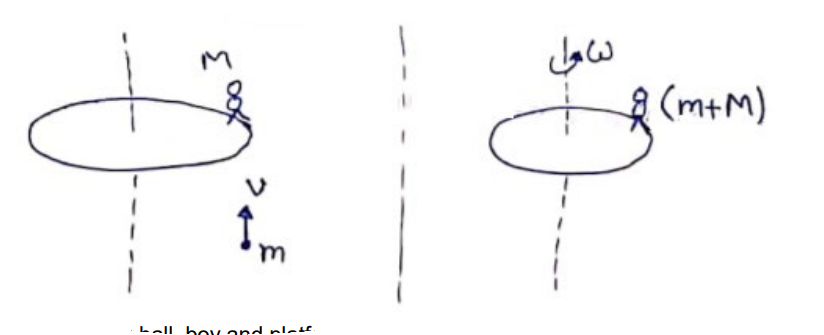
Considering ball, boy and platform as system $L_{i}=L_{f}$
$\mathrm{mvR}=\left[1+(\mathrm{M}+\mathrm{m})^{R^{2}}\right] \omega$
$\omega=\frac{m v R}{I+(M+m) R^{2}}$
