Solve the following systems of linear inequations graphically:

(i) Converting the inequations to equations, we obtain:

2x + 3y = 6, 3x + 2y = 6, x = 0, y = 0

2x + 3y =6:  This line meets the x-axis at (3,0) and the y-axis at (0, 2). Draw a thick line joining these points.

We see that the origin (0, 0) satisfies the inequation 2x + 3y ≤ 6

So, the portion containing  the origin represents the solution set of the inequation 2x + 3y ≤ 6

3x+2y =6:  This line meets the x-axis at (2, 0) and the y-axis at (0, 3). Draw a thick line joining these points.

We see that the origin (0,0) satisfies the inequation 3x + 2y ≤ 6.

So, the portion containing  the origin represents the solution set of the inequation 3x + 2y ≤ 6

Clearly, x ≥ 0, y ≥ 0 represents the first quadrant.

Hence. the shaded region in the figure represents the solution set of the given set of inequations.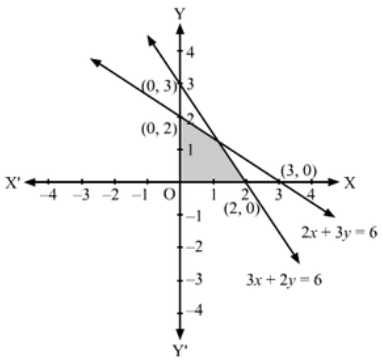

(ii)  Converting the inequations to equations, we obtain:
2x + 3y = 6, x + 4y = 4, x = 0, y = 0

2x + 3y =6:  This line meets the x-axis at (3, 0) and the y-axis at (0, 2). Draw a thick line joining these points.

We see that the origin (0,0) satisfies the inequation 2x + 3y ≤ 6.

So, the portion containing  the origin represents the solution set of the inequation 2x + 3y ≤ 6

x + 4y = 4:  This line meets the x-axis at (4, 0) and the y-axis at (0, 1). Draw a thick line joining these points.

We see that the origin (0,0) satisfies the inequation x + 4y ≤ 4.

So, the portion containing  the origin represents the solution set of the inequation x + 4y ≤ 4

Clearly, x ≥ 0, y ≥ 0 represents the first quadrant.

Hence, the shaded region in the figure represents the solution set of the given set of inequations.

(iii)  Converting the inequations to equations, we obtain:

$x-y=1, x+2 y=8,2 x+y=2, x=0, y=0$

$x-y=1$ : This line meets the $x$-axis at $(1,0)$ and the $y$-axis at $(0,-1)$. Draw a thick line joining these points.

We see that the origin $(0,0)$ satisfies the inequation $x-y \leq 1$ So, the portion containing the origin represents the solution set of the inequation $x-y \leq 1$

$x+2 y=8$ : This line meets the $x$-axis at $(8,0)$ and the $y$-axis at $(0,4)$. Draw a thick line joining these points.

We see that the origin $(0,0)$ satisfies the inequation $x+2 y \leq 8$ So, the portion containing the origin represents the solution set of the inequation $x+2 y \leq 8$

$2 x+y=2$ : This line meets the $x$-axis at $(1,0)$ and the $y$-axis at $(0,2)$. Draw a thick line joining these points.

We see that the origin $(0,0)$ does not satisfy the inequation $2 x+y \geq 2$ So, the portion that does not contain the origin represents the solution set of the inequation $2 x+y \geq 2$

Clearly, x ≥ 0, y ≥ 0 represents the first quadrant.

Hence, the shaded region in the figure represents the solution set of the given set of inequations.


(iv) Converting the inequations to equations, we obtain:

x + y =1, 7x + 9y = 63, x = 6, y = 5

$x+y=1$ : This line meets the $x$-axis at $(1,0)$ and the $y$-axis at $(0,1)$. Draw a thick line joining these points.

We see that the origin $(0,0)$ does not satisfy the inequation $x+y \geq 1$ So, the portion not containing the origin represents the solution set of the inequation $x+y \geq 1$

$7 x+9 y=63$ : This line meets the $x$-axis at $(9,0)$ and the $y$-axis at $(0,7)$. Draw a thick line joining these points.

We see that the origin $(0,0)$ satisfies the inequation $7 x+9 y \leq 63$ So, the portion containing the origin represents the solution set of the inequation $7 x+9 y \leq 63$

$x=6$ : This line is parallel to the $x$-axis at a distance 6 units from it.

We see that the origin $(0,0)$ satisfies the inequation $x \leq 6$ So, the portion containing the origin represents the solution set of the inequation $x \leq$ 6

$y=5$ : This line is parallel to the $y$-axis at a distance 5 units from it.

We see that the origin $(0,0)$ satisfies the inequation $y \leq 5$ So, the portion containing the origin represents the solution set of the inequation $y \leq 5$

Clearly, x ≥ 0, y ≥ 0 represents the first quadrant.

Hence, the shaded region in the figure represents the solution set of the given set of inequations.

(v) Converting the inequations to equations, we obtain:

2x + 3y = 35, x = 0, y = 0

2x + 3y = 35:  This line meets the x-axis at (17.5, 0) and the y-axis at (0, 35/3). Draw a thick line joining these points.

We see that the origin (0, 0) satisfies the inequation 2x + 3y ≤ 35 So, the portion containing  the origin represents the solution set of the inequation 2x + 3y ≤ 35

x = 2:  This line is parallel to the x-axis at a distance 2 units from it.

We see that the origin $(0,0)$ does not satisfy the inequation $x \geq 2$ So, the portion that does not contain the origin represents the solution set of the inequation $x \geq 2$

y = 3:  This line is parallel to the y-axis at a distance 3 units from it.

We see that the origin (0, 0) does not satisfies the inequation y ≥ 3 So, the portion opposite to the origin represents the solution set of the inequation y ≥ 3

Clearly, x ≥ 0, y ≥ 0 represents the first quadrant.

Hence, the shaded region in the figure represents the solution set of the given set of inequations.