In a $\Delta A B C, A D$ is the bisector or $\angle A$.
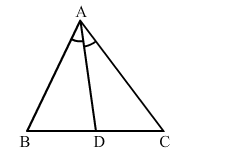
(i) If AB = 6.4 cm, AC = 8 cm and BD = 5.6 cm, find DC.
(ii) If AB = 10 cm, AC = 14 cm and BC = 6 cm, find BD and DC.
(iii) If AB = 5.6 cm, BD = 3.8 cm and BC = 6 cm, find AC.
(iv) If AB = 5.6 cm, AC = 4 cm and DC = 3 cm, find BC.
(i)
It is given that $\mathrm{AD}$ bisects $\angle \mathrm{A}$.
Applying angle - bisector theorem in $\triangle \mathrm{ABC}$, we get:
$\frac{\mathrm{BD}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}$
$\Rightarrow \frac{5.6}{\mathrm{DC}}=\frac{6.4}{8}$
$\Rightarrow \mathrm{DC}=\frac{8 \times 5.6}{6.4}=7 \mathrm{~cm}$
(ii)
It is given that $\mathrm{AD}$ bisects $\angle \mathrm{A}$.
Applying angle $-$ bisector theorem in $\triangle \mathrm{ABC}$, we get:
$\frac{\mathrm{BD}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}$
Let $\mathrm{BD}$ be $x \mathrm{~cm}$.
Therefore, $\mathrm{DC}=(6-x) \mathrm{cm}$
$\Rightarrow \frac{x}{6-x}=\frac{10}{14}$
$\Rightarrow 14 x=60-10 x$
$\Rightarrow 24 x=60$
$\Rightarrow x=2.5 \mathrm{~cm}$
Thus, $\mathrm{BD}=2.5 \mathrm{~cm}$
$\mathrm{DC}=6-2.5=3.5 \mathrm{~cm}$
(iii)
It is given that $\mathrm{AD}$ bisects $\angle \mathrm{A}$.
Applying angle $-$ bisector theorem in $\triangle \mathrm{ABC}$, we get:
$\frac{\mathrm{BD}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}$
$\mathrm{BD}=3.2 \mathrm{~cm}, \mathrm{BC}=6 \mathrm{~cm}$
Therefore, $\mathrm{DC}=6-3.2=2.8 \mathrm{~cm}$
$\Rightarrow \frac{3.2}{2.8}=\frac{5.6}{\mathrm{AC}}$
$\Rightarrow A C=\frac{5.6 \times 2.8}{3.2}=4.9 \mathrm{~cm}$
(iv)
It is given that $\mathrm{AD}$ bisects $\angle \mathrm{A}$.
Applying angle $-$ bisector theorem in $\triangle \mathrm{ABC}$, we get :
$\frac{B D}{D C}=\frac{A B}{A C}$
$\Rightarrow \frac{B D}{3}=\frac{5.6}{4}$
$\Rightarrow B D=\frac{5.6 \times 3}{4}$
$\Rightarrow B D=4.2 \mathrm{~cm}$
Hence, BC = 3 + 4.2 = 7.2 cm
