Question:
If $f(x)=[x]-\left[\frac{x}{4}\right], x \in R$, where $[x]$ denotes the
greatest integer function, then :
Correct Option: , 4
Solution:
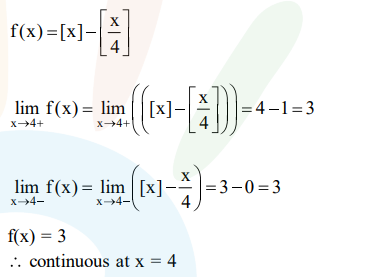
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
