Henry's constant (in kbar) for four gases $\alpha, \beta$, $\gamma$ and $\delta$ in water at $298 \mathrm{~K}$ is given below :
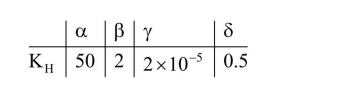
(density of water $=10^{3} \mathrm{~kg} \mathrm{~m}^{-3}$ at $298 \mathrm{~K}$ )
This table implies that:
Correct Option: , 2
(1) $\mathrm{P}_{\gamma}=\mathrm{K}_{\mathrm{H}} \mathrm{X}_{\mathrm{Y}}$
$\mathrm{P}_{\gamma}=2 \times 10^{-15} \times \frac{55.5}{55.5+\frac{1000}{18}}=2 \times 10^{-5} \mathrm{~K}$ bar
$=2 \times 10^{-2} \mathrm{bar}$
(2) $\mathrm{P}_{\delta}=\mathrm{K}_{\mathrm{H}} \mathrm{X}_{\delta}$
$\mathrm{P}_{\delta}=0.5 \times \frac{55.5}{55.5+\frac{1000}{18}}=.249 \mathrm{~K}$ bar $=249$ bar
(3) On increasing temperature solubility of gases decreases
(4) $\mathrm{K}_{\mathrm{H}} \downarrow$ solubility $\uparrow$ and lowest $\mathrm{K}_{\mathrm{H}}$ is for $\gamma$.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.