Solve this following

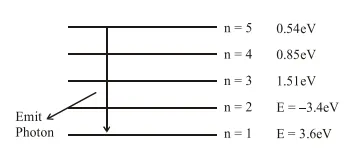
( $\Delta \mathrm{E})$ Releases when photon going from $\mathrm{n}=5$ to

$\mathrm{n}=\Delta \mathrm{E}=(13.6-0.54) \mathrm{eV}=13.06 \mathrm{eV}$

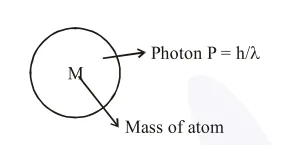
$\mathrm{P}_{\mathrm{i}}=\mathrm{P}_{\mathrm{f}}($ By linear momentum conservation $)$

$0=\frac{\mathrm{h}}{\lambda}-\mathrm{Mv}=\mathrm{V}_{\text {Recoil }}=\frac{\mathrm{h}}{\lambda \mathrm{M}}$   .............(I)

$\& \Delta \mathrm{E}=\frac{\mathrm{hc}}{\lambda}=\frac{\mathrm{hc}}{\lambda \mathrm{M}} \times \mathrm{M} \Rightarrow \mathrm{McV}_{\text {Recoil }}$

$\mathrm{V}_{\text {Recoil }}=\frac{\Delta \mathrm{E}}{\mathrm{Mc}}=\frac{13.06 \times 1.6 \times 10^{-19}}{1.67 \times 10^{-27} \times 3 \times 10^{8}}=4.17 \mathrm{~m} / \mathrm{sec}$